コレクション e^2x 積分 204637-Sinx e^2x 積分
Our calculator allows you to check your solutions to calculus exercises It helps you practice by showing you the full working (step by step integration) All common integration techniques and even special functions are supported//googl/JQ8NysTabular Integration the Integral of x^3*e^(2x)積分法|高校数学のつまずきやすい単元を徹底解説! 数学が苦手なお子さんは中学、高校とも学年が上がっていくごとに増えていきますよね。 今回は高校数学の中でも数Ⅲの積分について書いていきたいと思います。 微分法と同じく数Ⅱで学習した

积分公式和常用方法总结 Leemboy的博客 Csdn博客 积分公式
Sinx e^2x 積分
Sinx e^2x 積分-以下是部分指數函數的積分表 ∫ e c x d x = 1 c e c x {\displaystyle \int e^ {cx}\;dx= {\frac {1} {c}}e^ {cx}} ∫ a c x d x = 1 c ln a a c x ( a > 0 , a ≠ 1 ) {\displaystyle \int a^ {cx}\;dx= {\frac {1} {c\ln a}}a^ {cx}\qquad \qquad {\mbox { (}}a>0, {\mbox { }}a\neq 1 {\mbox {)}}}Please Subscribe here, thank you!!!




範例1 1 試解出下列微分方程dx Y 不嚴謹做法 把微分方程改寫為y Dx 兩邊同時積分y 之後可以推得 Ln Y X
· e^2x は、 t=2x と置いて置換してもよいけれど、牛刀の感がします。 e^2x を微分すると、 (2)* (e^2x)となるので、 e^2x の積分は、 (1/2)* (e^2x)と判明します。 79陽p»ç系微 }(99ç ˇ) Àj 31 }IV \ 函b含úi函b (t˜19 t˜26) V \ 函b含Nb函b (t˜27 t˜31) VI \ 函b含úb函b (t˜32 t˜38) UàŸ† (· · xe^ {2x}/√ (e^x1) 0,∞などの定積分 投稿日 21年6月6日 21年4月19日 投稿者 ぽじぽめ コメントをどうぞ <証明> 次の定積分の結果を用います。 詳細はこちらです。 (A) ・
E2x ⋅ e2x e 2 x ⋅ e 2 x Use the power rule aman = amn a m a n = a m n to combine exponents e2x2x e 2 x 2 x Add 2x 2 x and 2x 2 xSimplify e^ (2x)e^x e2x − ex e 2 x e x Nothing further can be done with this topic Please check the expression entered or try another topic e2x −ex e 2 x e x · \(e\) のべき乗は積分しても指数が変わらないので、\(e^{2x}\) を積分する方向で考えましょう。 ただし、\(e^{2x}\) は \(e^{f(x)}\) と \(f(x) = 2x\) の 合成関数 であることに注意します。
=∫1/2xd(e^2x) =1/2xe^2x1/2∫e^2xdx(这一步是分部积分法) =1/2xe^2x1/4∫e^2xd(2x) =1/2xe^2x1/4e^2xC =1/4(2x1)e^2xC · e2x とおいて再び部分積分の公式を使うと,上式は \begin {aligned} & 2x^2 e^ {2x} \left (4x \dfrac {1} {2}e^ {2x} \int 4 \dfrac {1} {2}e^ {2x} dx\right) \\ &= 2x^2 e^ {2x} 2x e^ {2x} e^ {2x} C \\ &= (2x^2 2x 1) e^ {2x} C \end {aligned} 2x2e2x −(4x21 e2x − ∫ 421 · 実際に2つの積分を計算します。 1つ目 ∫ − 1 − t 1 x 2 d x = − 1 x − 1 − t = − 1 1 t lim t → 0 1 t = ∞ となり、 ∫ − 1 − t 1 x 2 d x = ∞ ∫ t 1 1 x 2 d x = − 1 x t 1 = − 1 1 t lim t → 0 1 t = ∞ となり、 ∫ t 1 1 x 2 d x = ∞ となり、2つの広義積分はともに無限大に発散するので、 ∫ − 1 1 1 x 2 d x = ∞ となり、無限大に発散することがわかる。 (2つに分解した際に




實用特殊積分求法 每日頭條



X 2 E 2x的积分怎么求 数学作业 解题作业帮
積分電卓 解析積分を用いて所与の変数に対する関数の不定積分(アンチ導出)を計算する。 また、関数のグラフとその積分を描画することもできる。 計算された不定積分は、Cが任意の定数である関数F(x)Cのクラスに属することを覚えておいて下さい。Indefinite Integrals Pre Algebra Order of Operations Factors & Primes Fractions Long Arithmetic Decimals Exponents & Radicals Ratios & Proportions Percent Modulo Mean, Median & Mode Scientific Notation Arithmetics Algebra · 解答 本問題只要取變數變換 即可。 (2)利用 (1)試證明 解答 利用類似的想法,我們取 且 。 於是我們推得積分等於 (3)試證明 其中 。 證明 證明類似於 (2)。 (4)如果你學過對稱矩陣對角化的概念,你可以證明下列式子假設 是 正定方陣 (positive definite),則 證明 因為 是正定方陣,所以存在一個直交矩陣 使得 其中 是對角矩陣 。




E的2x次方的积分 对e的x次方求积分 E的积分怎么求




Ppt 第5 章不定积分powerpoint Presentation Free Download Id
· ∫ e t t d t \displaystyle\int\dfrac{e^t}{t}dt ∫ t e t d t ( − ∞\infty − ∞ から x x x までの定積分は指数積分と呼ばれる x x x の関数) ∫ 1 − k 2 sin 2 x d x \displaystyle\int\sqrt{1k^2\sin^2x}dx ∫ 1 − k 2 sin 2 x d x ( 0 0 0 から π 2 \dfrac{\pi}{2} 2 π までの定積分は第二種完全The Integral Calculator lets you calculate integrals and antiderivatives of functions online — for free! · e^x/(1e^2x)置換積分法を用いて解く問題なのですがわかりません、なにを置換すればいいのですか、教えてください 数学 解決済 教えて!goo



Http Www Math Ncu Edu Tw Yu Finacal96 Boards Lec32 Fc 96 Pdf



如何使用参数变化求解y Y 2y E 3x 教育小本子
· Integral of e^x/ (1e^2x) (substitution) Watch later Share Copy link Info Shopping Tap to unmute If playback doesn't begin shortly, try restarting your device You're signed outMore than just an online integral solver WolframAlpha is a great tool for calculating antiderivatives and definite integrals, double and triple integrals, and improper integrals It also shows plots, alternate forms and other relevant information to enhance your mathematical intuition Learn more about微積分I 14 53 被積分関数e2x はf(u) = eu,u = 2x と分解すれば合成関数f(g(x)) とみ なせる.u′ = g′(x) = 2 であるので,問題の不定積分を以下のように変形し 置換積分できるようにする. ∫ e2xdx = 1 2 ∫ e2x 2dx 1 2 ∫ eudu 1 2 eu C 1 2 e2x C 上の計算では定理46 を素直に適用した.この適用のしか




E2x积分 E的2x次方的不定积分是多少 三人行教育网 Www 3rxing Org




微积分学 不定积分 练习答案 维基教科书 自由的教学读本
· 不定積分の問題です。 ∫xe^(2x) dxを求めよ。 ヒントf(x)=x、g'(x)=e^(2x)とする。 この問題を部分積分法を使って解きたいのですが、分からないので詳しく教えて下さい。積分 e^x ∫ exdx ∫ e x d x ex e x の微分は, (ex)′ = ex ( e x) ′ = e x である. ⇒ ここ を参照 微分をしても ex e x のままなので, 微分の逆の操作である積分 をしても ex e x となるのである. ∫ exdx =exC ∫ e x d x = e x C積分 e^(x^2) 從負無窮到正無窮, Gaussian integral, integral of e^(x^2) from inf to inf, sqrt(pi), sqrt(π),blackpenredpen, math for fun




Methods Of Integration 積分的方法 Ppt Download



凑倒数积分 不定积分倒数代换 积分百科网
積分因子を使って解いてみましょう 例題4-3 線形1階微分方程式 \y' y = x\ を解きましょう。 解 答 まず, \(y\) の係数である \(1\) を積分します。 \(\displaystyle \int dx = x\) (このとき積分定数を付ける必要はありません)となって,積分因子は \(h(x) = e^x\) です。基本解は \(\phi(x) = e^{2x}\) と \(\psi(x) = e^{3x}\) です。 定数変化法は,特殊解の形が分かっていなくても使うことができる一方,積分の計算が面倒になる可能性があります。 · e^axを微分すると何?(e^2xやe^3xなど) 結論からいいますと、e^axを微分した場合にはae^axとなります。 これは(e^ax)'=(ax)'(e^ax)= ae^ax という流れの計算になるためです。 そのためaに具体的な数値の2や3を入れた式を考えていきますと ・e^2xの微分=2 e^2x



单变量微积分笔记11 微分和不定积分 我是8位的 博客园




不定积分有理函数分式分解
· First, find the general solution Let y = e^(ax) y" – 4y' 4y = 0 a^2 – 4a 4 (e^ax) = 0 (a^2 – 4a 4) = 0 a = 2 So y = Ke^(2x) is a general solution For the specific solution, it's tricky I thought at first you could use the form y = (axb) e^(2x), but you need an x^2 term 積分の公式微分積分 不定積分を求める e^ (2x) e2x e 2 x 多項式を x x の関数で表現する f (x) = e2x f ( x) = e 2 x 関数 F (x) F ( x) は導関数 f (x) f ( x) の不定積分を計算して求めることができます。 Error parsing MathML error on line 1 at column 150 Entity 'int' not defined Error parsing MathML error on line 1 at column 150 Entity 'int' not defined 整数を設定して解きます。 Error parsing MathML error on · Proportionality constants are written within the image sin θ, cos θ, tan θ, where θ is the common measure of five acute angles In mathematics, the trigonometric functions (also called circular functions, angle functions or goniometric functions) are real functions which relate an angle of a rightangled triangle to ratios of two side lengths



數學筆記11 微分和不定積分 It閱讀



下の問題の定積分の求め方教えて欲しいです E 2x は微分したとき 2x Yahoo 知恵袋
積分 {e^ (2x)}sinx ∫ e2xsinxdx ∫ e 2 x sin x d x の積分を 部分積分法 を用いて計算する. ∫ e2xsinxdx = ∫ (1 2e2x)′ sinxdx = 1 2e2xsinx−∫ 1 2e2x(sinx)′dx = 1 2e2xsinx−∫ 1 2e2xcosxdx = 1 2e2xsinx− 1 2 ∫ e2xcosxdx ・・・・・・(1) ∫ e 2 x sin x d x = ∫ ( 1 2 e 2 x) ′ sin x d x = 1 2 e 2広義積分 (携帯版)メニューに戻る (PC版)メニューに戻る *** 大区分 *** 数Ⅰ・A 数Ⅱ・B 数Ⅲ 高卒・大学初年度 *** 中区分 *** ベクトル・行列 連立方程式 複素数 関数・数列 微分 積分 微分方程式 統計 maxima ※ 高卒から大学初年度レベル の 「積分不定積分を計算する: x^5 dxの積分 x^2 sin^3 x の積分 ∫e^t sin (5t) 基本項では表せない不定積分を計算する: e^ (t^2)の積分 1/sqrt (1u^4)を積分する 与えられた関数を含む積分の表を生成する: cos (u)を含む積分




如何画出函数y E 2x 的图像 百度经验
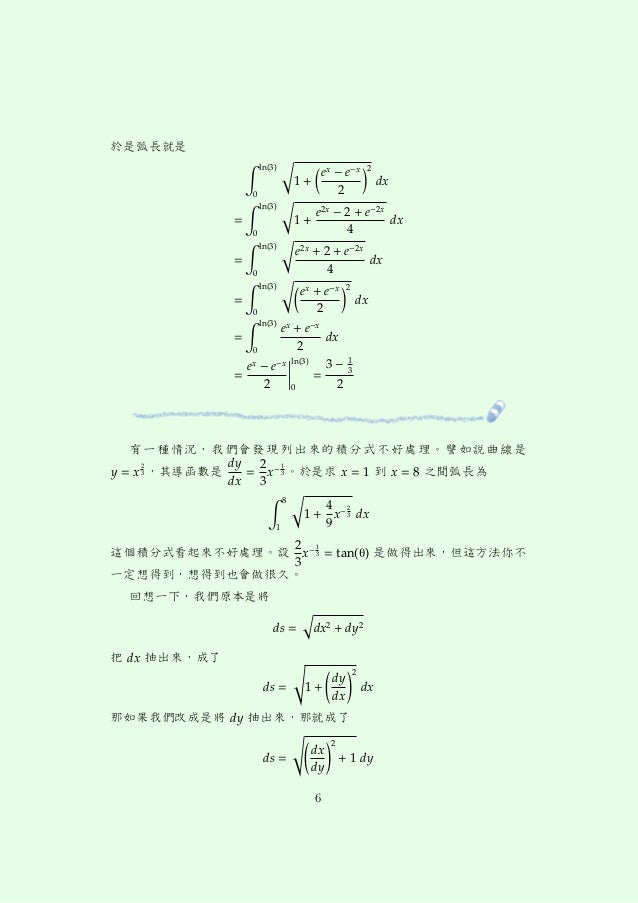



曲線弧長
Ejercicio resuelto de cálculo integral, por el método de integración por partes x e^2x dx · すると (e^2x)の微分=(e^2x)' = (2x)' (e^2x) =2e^2x と計算できました。2x乗の係数が微分により前に出てくることに気を付けるといいです。 ・積分の場合 一方で積分の場合でも基本的には同様に対処するといいです。 ∫e^2x dx= 1/2 e^2x Cとなります。 · e^2xを積分すると 1/2・e^2x になりますか? 途中式を教えていただけないでしょうか? 数学 Y=e^2x^2の微分 Y=e^2x^2 ←(y=eの2x乗の xの二乗) =(4)(e^2x^2)(4)(4x)(e^2x^2) =(4e^2x^2)(16x^2)(e^2x^2) =(4e^2x^2)(4x21) という問題と回答なのですが、 合成関数?
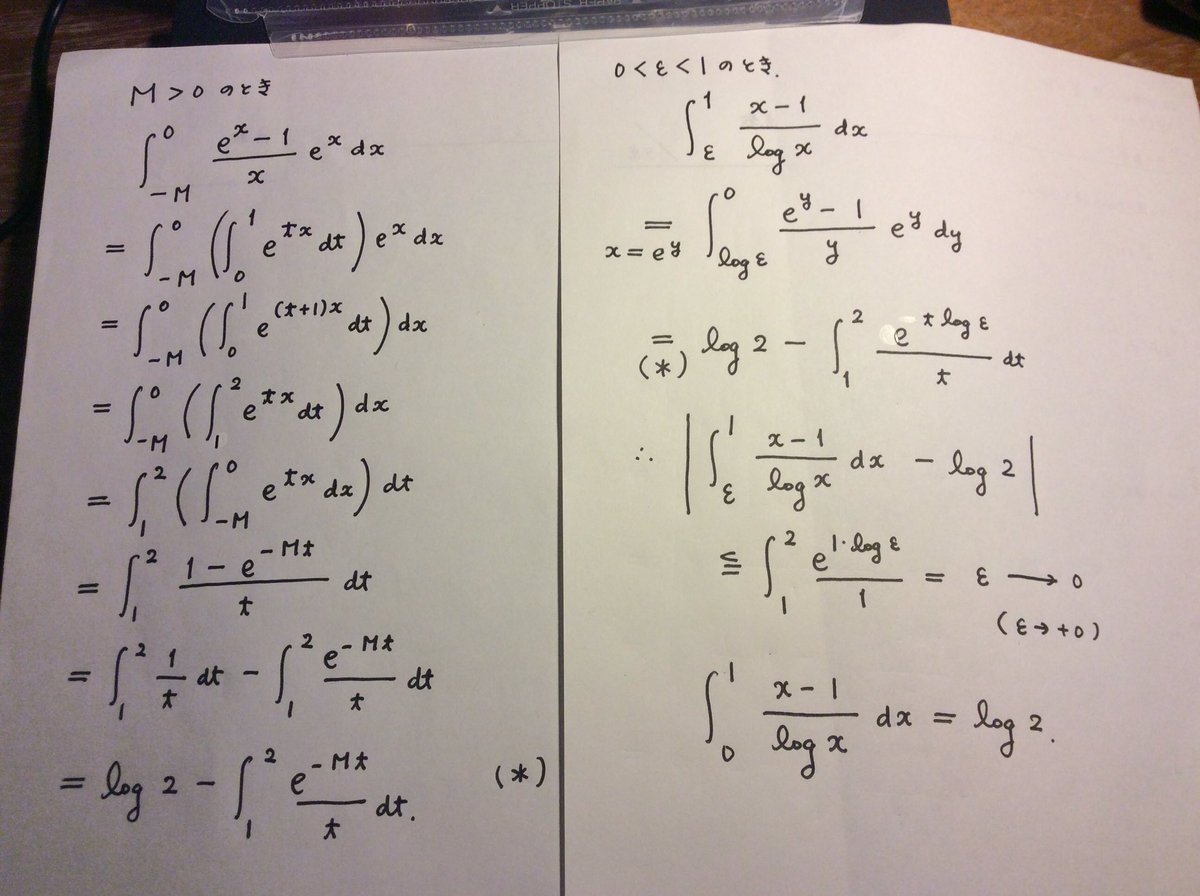



整数問題bot あってると思います 自分はe 2x E X X E 2x 1 X E X 1 Xとしてやることを想定してました そういう重積分の発想ってコツとかあるんですか なんか複素積分するのが定石みたいな問題をそういうやり方で解けるようになりたい T Co




高等数学微积分 北大版 Pages 101 150 Flip Pdf Download Fliphtml5



E的负x次方分之一图像 信息阅读欣赏 信息村 K0w0m Com




高斯積分 積分e X 2 中文版 Gaussian Integral Integral Of E X 2 Youtube




E的负x平方的积分 在线图书馆




积分公式和常用方法总结 Leemboy的博客 Csdn博客 积分公式




Re 微積 請問羅必達與瑕積分兩題 Math板 Web批踢踢 引述 Q0u04




E的负2x次方积分 在线图书馆




第5章 6 瑕積分




Ex 7 2 Integrate E 2x E 2x E 2x E 2x Ex 7 2




微積分分部積分 考試板 Dcard




微積分6 2 分部積分法 斯達奈異度空間 張耀英數理教室 痞客邦



3



这72道积分题目会积了 绝对是高高手 答案 0 知乎




求不定积分ln E X 根号下 1 E 2x Dx 雨露学习互助




X2ex积分 求不定积分 E X 47 X 2 Dx 三人行教育网 Www 3rxing Org




Eの2x乗の微分や積分は Eの3x乗の微分や積分は Eのマイナスx乗の微分や積分は E 2x E 3x E X ウルトラフリーダム



急求数学帝解答exp X 1 Exp 2x 积分过程我知道答案是atan 1 Exp X 1 Exp X 但是自己积分怎么就积分 不出来呢 我是令t Exp X 然后化成1 T 2 1 1 T 2 积分 但是这样的结果是 Exp 1 Arctan Exp X 作业 慧海网
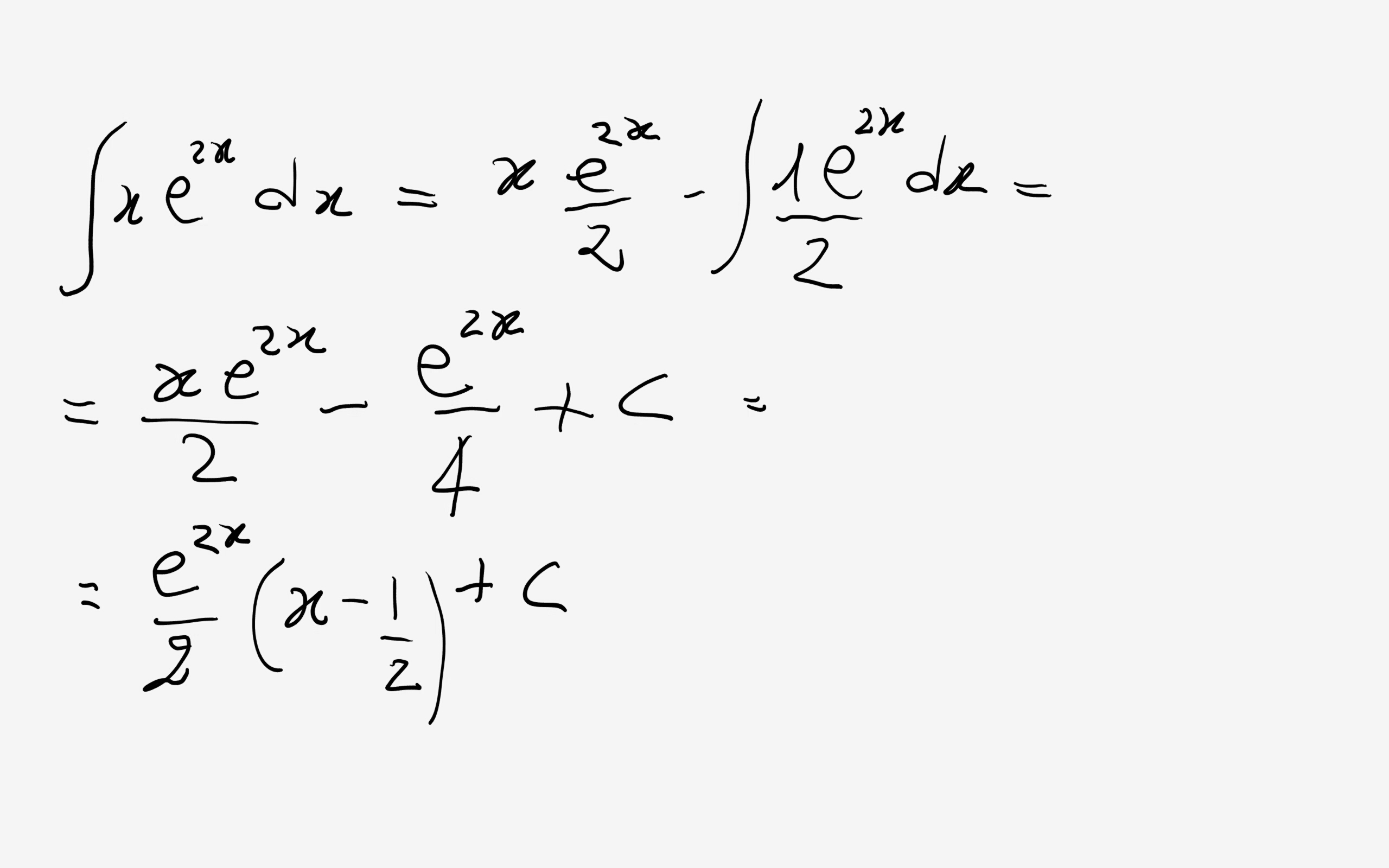



How Do You Integrate Xe 2x Dx Socratic



E的x次方 文章阅读中心 急不急图文 Jpjww Com



不定积分e 2x Sin 3x Dx怎么算 要用分部积分法 微思作业本



E的x次方积分 万图壁纸网



求 E 2x 1 E 2x 2 Dx的积分 数学作业 解题作业帮




朱式幸福 106年公務人員高等考試三級考試 微積分 微分方程詳解



单变量微积分笔记11 微分和不定积分 我是8位的 博客园




1 X 29 X 2 Dx2 X 2 1 急 不确定积分 多次操作 详细过程 好加点o 365bet送彩金 365注单审核不能提款




不定积分 二元一次方程组




数学 计算积分 2x1 E 不定积分 365bet正网娱乐 365bet怎么进不去了



E的负x次方分之一图像 信息阅读欣赏 信息村 K0w0m Com



高等数学 微积分中的不定积分 知乎




範例1 1 試解出下列微分方程dx Y 不嚴謹做法 把微分方程改寫為y Dx 兩邊同時積分y 之後可以推得 Ln Y X




高斯積分 積分e X 2 中文版 E X 2微分



估计积分的值 4 S 0 2 E X 2 X Dx 数学竞赛平台 数学帮 Math110




E Axを微分すると何 E 2xやe 3xなど E Ax B Y E 2x 1など を微分するとどう Ae Bxを微分するとどうなるか ウルトラフリーダム



分部积分法 简书



Sin X 2 Cos X 2 の実積分 フレネル積分 を複素積分で解く ばたぱら




Cos求导cos X和cosx 一样吗 E X 2 定积分推导



積分 E 2x Sinx




实验五用mathematica软件计算一元函数的积分




高斯積分 維基百科 自由的百科全書




数学 固定积分 Bet365 手机网址 365betvip5 365bet体育在线手机版下载




Xexdx的不定积分 搜狗搜索




定积分 E X 2 Dx 搜狗搜索




不定积分sin2xdx 不定积分 Sin2xdx



E 2x 積分 達人專欄 Uvyo




Solved 1算出下列積分j3xdr A 3x C B 3x2 C C 를x2 Chegg Com




第六章定积分下载 Word模板 爱问共享资料




Tabular Integration The Integral Of X 3 E 2x Youtube




三重積分



How Do You Integrate E 3x Sin 2x Dx Socratic




Ex 7 2 Integrate E 2x E 2x E 2x E 2x Ex 7 2




全导数例题




超越函数e X 2 的定积分 Norstc的博客 Csdn博客




不定积分e X Sin 2xdx 和e 2x Sinxdx 雨露学习互助




E 2x 積分 達人專欄 Uvyo




高等数学微积分 北大版 Pages 101 150 Flip Pdf Download Fliphtml5



E X 1 E 2x Dxの不定積分を求めよという問題で Yahoo 知恵袋



22考研 不定积分的积分法 一 公式



Integral E 2x 1 Youtube




對數函數積分表 維基百科 自由的百科全書



高斯積分 積分e X 2 中文版 E X 2微分




1 E 2x 2e X Dxがわかりません T E Xと置きました 答えは1番 高校 教えて Goo




What Is The Integration Of 1 Xe X Quora



求下列不定积分 Arctan E X E 2x Dx 作业 慧海网



Http Info Public Com Tw Prog Gavin Reference Checktype Asp Id 5b 25 2b 21 2e 3a No Rf Jrt




微积分学 不定积分 练习答案 维基教科书 自由的教学读本




Ppt 指數與對數的積分powerpoint Presentation Free Download Id




高斯積分 積分e X 2 中文版 Gaussian Integral Integral Of E X 2 Youtube




Ex 7 6 21 Integrate E 2x Sin X Using Integration By Parts




Int E 3x E X E 4x E 2x 1 Dx



X的三分之一乘以e的x次方的不定积分 图片欣赏中心 急不急图文 Jpjww Com




数学 固定积分 Best365体育备用网址 Bet 36体育 bet官




Eの 2x乗の積分ってどうやりますか 紙に書いて送って欲しいです Clear



求不定积分se 4xsqrt 1 E 2x Dx 数学竞赛平台 数学帮 Math110




想請問直接對 2x 作微分這樣是對的嗎還是一定只能對未知數做微分 Clear




My Publications 积分表公式推导 Page 84 85 Created With Publitas Com



3



E的x次方积分 万图壁纸网




X 2 E X 2 X 2 Dx用于积分 365结算错误我又投注了 365bet平台赌场




有哪些不定積分的運算 心算 技巧 Getit01
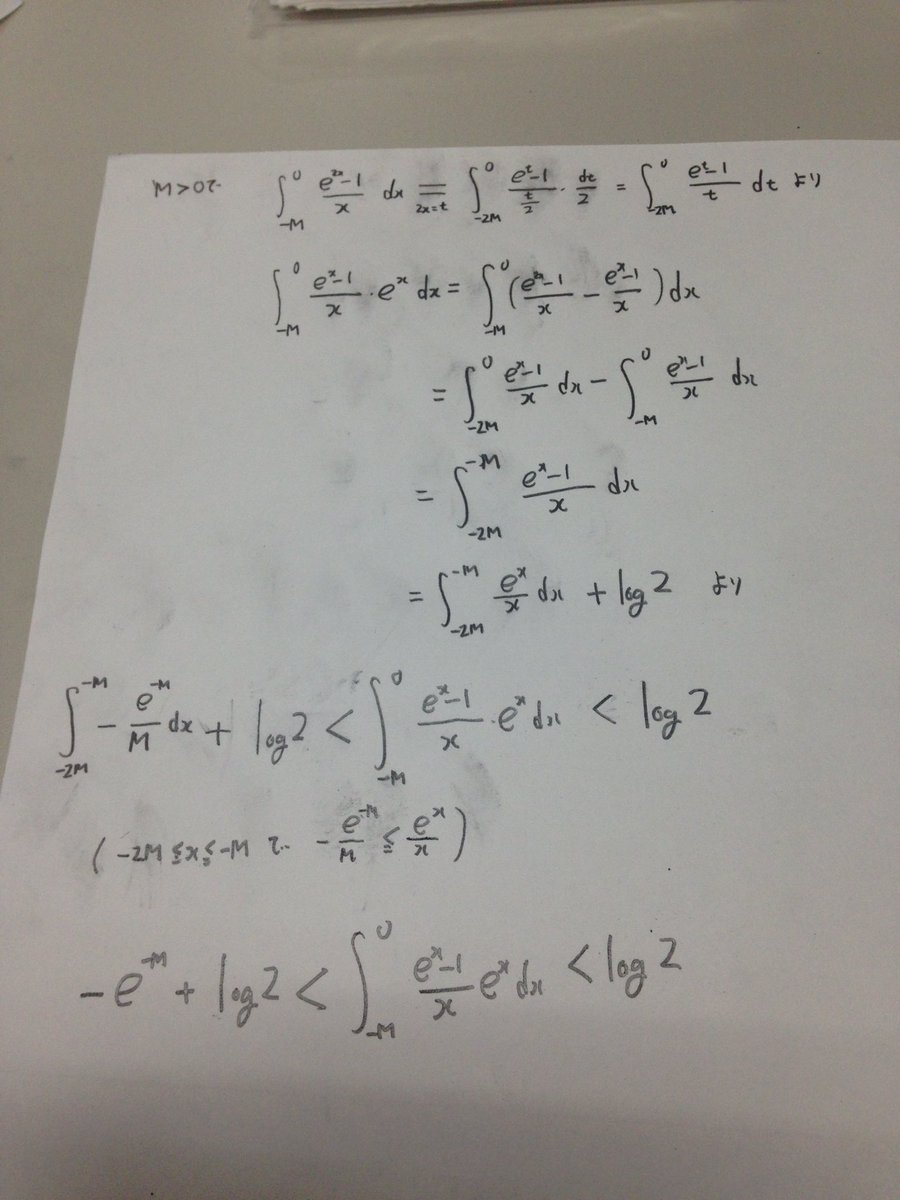



整数問題bot あってると思います 自分はe 2x E X X E 2x 1 X E X 1 Xとしてやることを想定してました そういう重積分の発想ってコツとかあるんですか なんか複素積分するのが定石みたいな問題をそういうやり方で解けるようになりたい T Co
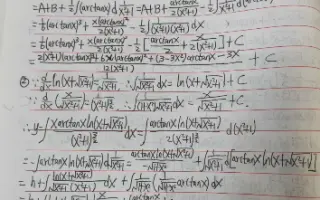



不定积分分部积分法先写别问 搜索结果 哔哩哔哩 Bilibili




範例1 1 試解出下列微分方程dx Y 不嚴謹做法 把微分方程改寫為y Dx 兩邊同時積分y 之後可以推得 Ln Y X




如何画出函数y E 2x 的图像 百度经验




求不定积分 1 二次根号下 E的x次方加二 雨露学习互助




1 Int X25x1 3 2x5 Dx 2 In See How To Solve It At Qanda


コメント
コメントを投稿